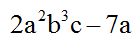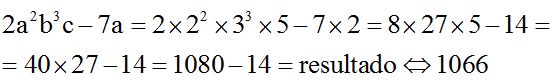Polinomios

Un polinomio es una expresión algebraica de la forma:

P(x) = a_n xⁿ + a_{n − 1} x^{n − 1} + a_{n − 2} x^{n − 2}+ ... + a₁x¹ + a₀

Siendo:

a_n, a_n−1 ... a₁, a_onúmeros, llamados coeficientes

n un número natural

x la variable o indeterminada

a_n es el coeficiente principal

a_o es el término independiente

CLASIFICACION DE LAS EXPRESIONES ALGEBRAICAS

Monomio

Es una expresión algebraica que consta de un solo término.
Ejemplo

12m⁴

Binomio

Polinomio binomio: Es el que consta de dos términos.

Ejemplo 

x² - y²

Trinomio 

Polinomio trinomio: Es el que consta de  tres términos.

Ejemplo

 x² - 10x + 25

Polinomio

Es una expresión algebraica que consta de más de un término.

Ejemplos

1) x² - y²

2) x² - 10x + 25

3) 2x⁴ + 5x⁵ - 54x – 135

Grado de un término algebraico

Grado de un termino

El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x.

Según su grado los polinomios pueden ser de:

TIPO	EJEMPLO
PRIMER GRADO	P(x) = 3x + 2
SEGUNDO GRADO	P(x) = 2x2 + 3x + 2
TERCER GRADO	P(x) = x3 − 2x2 + 3x + 2

Grado absoluto: se obtiene sumando todos los exponentes de las variables.

EJEMPLO:

Grado = 5 + 4 + 7 

Grado = 16

Tipos de polinomios

1Polinomio nulo

Es aquel polinomio que tiene todos sus coeficientes nulos.

P(x) = 0x² + 0x + 0

2Polinomio homogéneo

Es aquel polinomio en el que todos sus términos o monomios son del mismo grado.

P(x) = 2x² + 3xy

3Polinomio heterogéneo

Es aquel polinomio en el que no todos sus términos no son del mismo grado.

P(x) = 2x³ + 3x² − 3

4Polinomio completo

Es aquel polinomio que tiene todos los términos desde el término independiente hasta el término de mayor grado.

P(x) = 2x³ + 3x² + 5x − 3

5Polinomio incompleto

Es aquel polinomio que no tiene todos los términos desde el término independiente hasta el término de mayor grado.

P(x) = 2x³ + 5x − 3

6Polinomio ordenado

Un polinomio está ordenado si los monomios que lo forman están escritos de mayor a menor grado.

P(x) = 2x³ + 5x − 3

7Polinomios iguales

Dos polinomios son iguales si verifican:

Los dos polinomios tienen el mismo grado.

Los coeficientes de los términos del mismo grado son iguales.

P(x) = 2x³ + 5x − 3

Q(x) = 5x − 3 + 2x³

8Polinomios semejantes

Dos polinomios son semejantes si verifican que tienen la misma parte literal.

P(x) = 2x³ + 5x − 3

Q(x) = 3x³ + 7x − 2


OBSERVA EL VIDEO Y COMENTA

Fuentes:

http://www.vitutor.com/ab/p/a_4.html

http://www.ceibal.edu.uy/contenidos/areas_conocimiento/mat/algebra1/grado_de_un_trmino_algebraico.html

https://www.youtube.com/watch?v=7pTvnnA7CCo

Suma de polinomios

Para sumar dos polinomios se suman los coeficientes de los términos del mismo grado.

P(x) = 2x³ + 5x − 3      Q(x) = 4x − 3x² + 2x³

1Ordenamos los polinomios, si no lo están.

Q(x) = 2x ³− 3x² + 4x

P(x) + Q(x) = (2x³ + 5x − 3) + (2x³ − 3x²+ 4x)

2Agrupamos los monomios del mismo grado.

P(x) + Q(x) = 2x³ + 2x³ − 3 x² + 5x + 4x − 3

3Sumamos los monomios semejantes.

P(x) + Q(x) = 4x³ − 3x² + 9x  − 3

También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.

P(x) = 7x⁴ + 4x² + 7x + 2      

Q(x) = 6x³ + 8x +3

P(x) + Q(x) = 7x⁴ + 6x³ + 4x² + 15x + 5

OBSERVA EL VIDEO PARA ENTENDER MEJOR LA SUMA DE POLINOMIOS.

SUMA DE POLINOMIOS CON FRACCIONES

Fuente:  http://www.vitutor.com/ab/p/a_5.html

https://www.youtube.com/watch?v=szmjdS1Whz0
https://www.youtube.com/watch?v=uzWkg59D_Kg

PRESENTACION DE SUMA DE POLINOMIOS

RESTA DE POLINOMIOS

 Propiedades de los reales en la resta o sustracción

Al efectuar sustracciones o restas deben considerarse las siguientes reglas de los signos:

a) Si el minuendo y el sustraendo son positivos, y el minuendo es mayor que el sustraendo, se efectúa la resta y el resultado es positivo.

Ejemplo:

28.7 – 11.2 = 17.5

b) Si el minuendo y el sustraendo son positivos, y el minuendo es menor que el sustraendo, se efectúa la resta y el resultado es negativo.

Ejemplo:

11.2 – 28.7 = –17.5

c) Si el minuendo es negativo y el sustraendo es positivo, se efectúa la suma de ambos números y al resultado se le pone el signo menos.

Ejemplo:

–28.1 – 11.2 = –39.3

d) Restar un número positivo es lo mismo que sumar un número negativo.

Ejemplo:

28.7 – 11.2 = 28.7 + (–11.2) = 17.5

e)  Restar un número negativo es lo mismo que sumar un número positivo.

Ejemplo:

28.7 – (–11.2) = 28.7 + 11.2 = 39.3 

f) La resta no tiene todas las propiedades de la suma:

La resta no es una operación conmutativa:

Ejemplo:

52.4 – 31.2 = 21.2, y ese resultado es distinto de 31.2 – 52.4 = –21.2

      OBSERVA EL VIDEO

bibliografias

https://www.portaleducativo.net/segundo-medio/2/numeros-reales-y-propiedades

Multiplicacion de polinomios

1. Multiplicación de un número por un polinomio

Es otro polinomio que tiene de grado el mismo del polinomio y como coeficientes el producto de los coeficientes del polinomio por el número y dejando las mismas partes literales.

Ejemplo

3 · (2x³ − 3x² + 4x − 2) = 6x³ − 9x² + 12x − 6

2. Multiplicación de un monomio por un polinomio

Se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio.

Ejemplo:

3x² · (2x³ − 3x² + 4x − 2) =
= 6x⁵− 9x⁴ + 12x³ − 6x²

3. Multiplicación de polinomios

Este tipo de operaciones se puede llevar a cabo de dos formas distitnas.

Mira la demostración con el siguiente ejemplo:

P(x) = 2x² − 3       Q(x) = 2x³ − 3x² + 4x

OPCIÓN 1

1Se multiplica cada monomio del primer polinomio por todos los elementos del segundo polinomio.

P(x) · Q(x) = (2x² − 3) · (2x³ − 3x² + 4x) =
= 4x⁵ − 6x⁴ + 8x³ − 6x³+ 9x² − 12x =

2Se suman los monomios del mismo grado.

= 4x⁵ − 6x⁴ + 2x³ + 9x² − 12x

3Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.

Grado del polinomio = Grado de P(x) + Grado de Q(x) = 2 + 3 = 5

OPCIÓN 2

Fuente: http://www.vitutor.com/ab/p/a_6.html

DIVISION DE POLINOMIOS

Para explicar la división de polinomios nos valdremos de un ejemplo práctico:

P(x) = x⁵ + 2x³ − x − 8         Q(x) = x² − 2x + 1

P(x) :  Q(x)

A la izquierda situamos el dividendo. Si el polinomio no es completo dejamos huecos en los lugares que correspondan.

A la derecha situamos el divisor dentro de una caja.

Dividimos el primer monomio del dividendo entre el primer monomio del divisor.

x⁵ : x² = x³

Multiplicamos cada término del polinomio divisor por el resultado anterior y lo restamos del polinomio dividendo:

Volvemos a dividir el primer monomio del dividendo entre el primer monomio del divisor. Y el resultado lo multiplicamos por el divisor y lo restamos al dividendo.

2x⁴ : x² = 2 x²

Procedemos igual que antes.

5x³ : x² = 5 x

Volvemos a hacer las mismas operaciones.

8x² : x² = 8

10x − 16 es el resto, porque su grado es menor que el del divisor y por tanto no se puede continuar dividiendo.

x³ + 2x² + 5x + 8 es el cociente.


video de división de polinomios

fuentes: http://youtube.com/watch?v=Bg3ZzssmwKI

VALOR NUMERICO

Se trata de una simple sustitución de números por letras para después hacer los cálculos indicados por la expresión y obtener así un resultado:

Ejemplo:

Dada la expresión: 

Solución:

Sustituimos las letras por los números teniendo en cuenta los signos aritméticos:

Respuesta: 1066

      OBSERVA EL VIDEO